Generative Model
Depending on whether annotation is available, machine learning mathods can be cetergorized as supervised and unsupervised learning. The different modeling over the distribution $x$ can roughly divide these methods into two catergory: generative and discriminative. In supervised learning, the most common one is discriminative which models the conditional probability $p_\theta(y|x)$ parameterized by $\theta$. With $\theta$ learnt from back propagation over the samples, models directly predict $y = p_\theta(y|x)$. Gernerative model, on the other hand, models the joint probability of $p(x, y)$ and predict $y=p(y|x)=\frac{p(x, y)}{p(x)}$ . Knowing what generative model cares about, we focus on the unsupervised generative model that’s used to generate images as real as possible.
Modeling over p(x)
Given a distribution $p_\theta(x)$ parameterized by $\theta$, we denote the true distribution as $p_{\theta^\ast}(x)$ . To generate sample $x$ without no annotation as close as possible to $p_{\theta^\ast}(x)$ , we want to find the optimal $\theta^\ast$. That is, We want to find a $\theta$ that maximize the log probability of $p_\theta(x)$ with $x\sim p_{\theta^\ast}(x)$ .
$$\theta^* = \operatorname*{argmax}_\theta p_{x\sim p_{\theta^*}(x), \theta}(x)\\ $$Empirically, this equals to maximize the likelihood of joint probability of all training samples:
$$\theta^* = \operatorname*{argmax}_\theta \prod_{i=1}^{m} p_{\theta}(x_i)\\ $$This can be rewrite as maximization of log likelihood and be approximated by the samples drawn from $p(x)$:
$$ \theta^* = \operatorname*{argmax}_\theta \log (p_{x\sim p_{\theta^*}(x), \theta}(x))\\ =\operatorname*{argmax}_\theta \log (\prod_{i=1}^m p_\theta(x_i))\\ =\operatorname*{argmax}_\theta \sum_{i=1}^m \log p_\theta(x_i) \\ $$This can also be seem as maximizing the expection of log likelihood with respect to $p_{\theta^\ast}(x)$, which can be rewrite as minimization of cross entropy between the two distributions. This equals to minimization of KL Divergence between the two distributions since the entropy of $p_{\theta^\ast}(x)$ is fixed as a constant:
$$ \theta^* = \operatorname*{argmax}_\theta E_{x\sim p_{\theta^*}(x)}[\log p_\theta (x)]\\ = \operatorname*{argmin}_\theta \int_x p_{\theta^*}(x) \log \frac{1}{p_\theta (x)} dx\\ \Longleftrightarrow \operatorname*{argmin}_\theta \int_x p_{\theta^*}(x) \log \frac{1}{p_\theta (x)} dx - \int_x p_{\theta^*}(x) \frac{1}{\log p_{\theta^*}(x)} dx\\ = \operatorname*{argmin}_\theta \int_x p_{\theta^*}(x) \log \frac{p_{\theta^*}(x)}{p_\theta (x)} dx\\ = \operatorname*{argmin}_\theta D_{KL}(p_{\theta^*}(x)||p_\theta (x)) $$A taxonomy of deep generative models
We refer to NIPS2016 2016 Tutorial on GAN by Ian for taxonomy of generative models.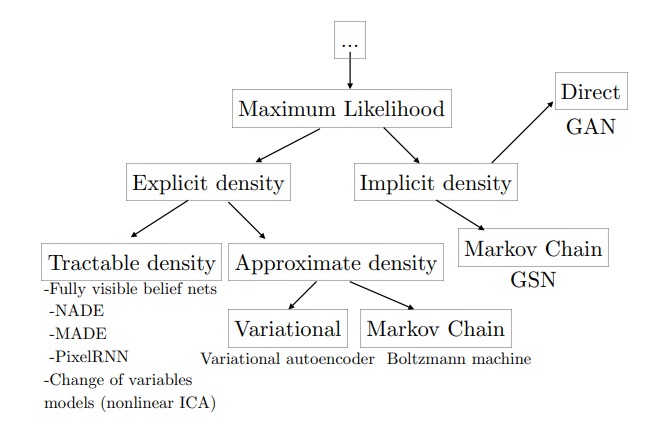
Now that we have the goal: maximization the log likelihood of $p_{x\sim p_{\theta^\ast}(x), \theta}(x)$. One of the biggest problem is how to define $p_\theta(x)$. Explicit density models define an explicit density function $p_\theta(x)$, which can be directly optimized through backprop. The main difficulty present in explicit density models is designing a model that can capture all of the complexity of the data to be generated while still maintaining computational tractability.